Rätsel mit 3 Quadraten + Dreiecken + Winkeln

von

Zur Abwechslung hier mal etwas zum Knobeln. Dieses mathematische Rätsel mit 3 Quadraten + Dreiecken + Winkeln habe ich vorhin beim Stöbern im Internet gefunden. Unter dem Titel Drei Quadrate und Winkel darin wurde es vor kurzem im Spektrum der Wissenschaft veröffentlicht.

3-quadrat-winkel

Der Ursprung dieses Rätsels geht auf eine Knobelei von Martin Gardner zurück, der es vor rund 50 Jahren im Scientific American veröffentlicht hat.

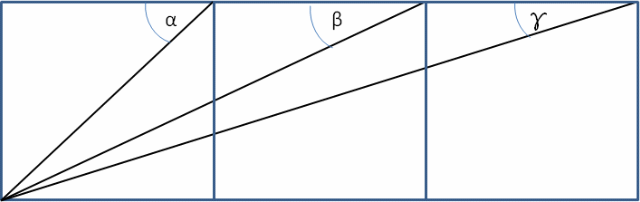
Gegeben sind drei nebeneinander liegende Quadrate. Verbindet man den Eckpunkt unten links mit den gegenüberliegenden Eckpunkten der Quadrate, so entstehen drei Winkel (α, β, γ). Die Summe des größeren Winkels ist gleich der Summe der zwei anderen Winkel. α = β + γ

Das Rätsel ist durchaus kniffelig. Nach seiner Veröffentlichung haben sich seinerzeit Dutzende von Rätselknackern mit eigenen Lösungsmöglichkeiten gemeldet.

Rechnet man die Winkel einmal klassisch nach, so erhält man α=45°, β=25,56…° und γ= 18,43…°

Siehe auch Drei Quadrate Satz oder Problem des Monats April 2005 mit Lösung
Der erste Beweis basiert witzigerweise auf einer Phythagroräischen Zahlentripel Dreieckskonstruktion (3,4,5).

6 Gedanken zu „Rätsel mit 3 Quadraten + Dreiecken + Winkeln“

  1. Lieber Herr Steffens, da Sie immer wieder nach der Anwendbarkeit fragen, stelle ich Ihnen die Frage nach der Anwendbarkeit der Lösung dieses Rätsels in meinem Leben.

    Antworten

    • Ich zwinge hier niemanden diese Aufgabe zu lösen. Das ist vollkommen freiwillig. Diese Freiwilligkeit sehe ich nicht bei den Aufgaben bzw. Hausaufgaben im Mathematik Unterricht 😉

      Antworten

  3. Ich sehe 3 Dreiecke, mit selbem Eckpunkt A unten links. Die Winkel sind Wechselwinkel an diesem Punkt.

    Mit Seite a des Quadrats gilt dann:

    alpha = arctan(a/a) = arctan(1) = 45 Grad

    beta = arctan(a/2a) = arctan(1/2) = 26,57 Grad

    gamma = arctan(a/3a) =arctan(1/3) = 18,43 Grad

    45 Grad = 26,57 Grad + 18,43 Grad

    QED

    Antworten

Schreibe einen Kommentar