Heiß geliebt oder schwer gehasst. Die drei binomischen Formeln gehören neben dem Satz des Pythagoras zu den bekanntesten, aber nicht zu den beliebtesten mathematischen Formeln/Sätzen der Schulzeit. Viele Schüler dürften diese besondere Mischung aus Quadrat, Summe und Differenz von Zahlen eher nicht mögen. Dabei können sie Schülern z.B. beim Lösen quadratischer Gleichungen hilfreich zur Seite stehen.
Die drei binomischen Formeln
- 1. Binomische Formel: (a+b)² = a²+2ab+b²
- 2. Binomische Formel: (a-b)² = a²-2ab+b²
- 3. Binomische Formel: (a+b)(a-b) = a²-b²
Die 1. Binomische Formel ist die am leichtesten zu merkende der drei Formeln. Die 2. Binomische Formel ist etwas tricky, sie ist der ersten Formel recht ähnlich, nur das Vorzeichen des mittleren Terms ist negativ. Die 3. Binomische Formel ist die nachgefragteste Variante, aufgrund der unterschiedlichen Vorzeichen in den beiden Klammern hebt sich die mittlere Komponente weg. Die nachfolgende Grafik veranschaulicht das unterschiedliche Suchinteresse bzgl. der drei Formeln.
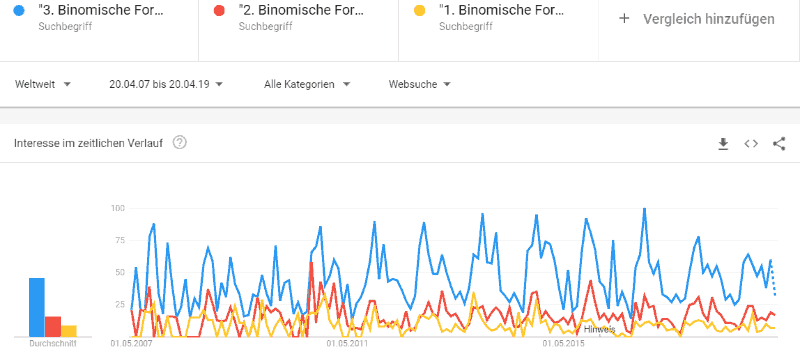
Ihr seht anhand der obigen Google Trends Kurvenverläufe, dass die dritte binomische Formel weit häufiger auf Google gesucht wird als die zweite und dritte Formel zusammen.
Die Herleitung der drei binomischen Formeln ist eigentlich ganz elementar mit Multiplikation, Addition und Auflösung der Klammern und unter Zuhilfenahme des Distributivgesetzes, Assoziativgesetzes und Kommutativgesetzes zu führen. D.h. die entsprechenden Terme multiplizieren, umklammern, addieren und umstellen – fertig!
Eine echte Hilfe zum Merken und Herleiten der binom. Formeln kann das Betrachten des folgenden Videos des Dorfuchses sein.
Wer sich das Video ein paar mal reingezogen hat, der wird diesen Ohrwurm und damit die Formeln mitsamt Beweis so schnell nicht mehr vergessen 🙂
Die drei binomischen Formeln im Beweis
| 1. Binomische Formel | 2. Binomische Formel |
|
|
Die erste und die zweite binomische Formel sind fast identisch und unterscheiden sich lediglich beim Vorzeichen des Summanden bzw. des mittleren Summen Terms. Die dritte Formel hingegen gewinnt ihren Charme durch die gegenseitige Auslöschung der mittleren Terme.
| 3. Binomische Formel |
|
In der Schule werden die binomischen Formeln typischerweise in der 7. oder 8. Klasse eingeführt. Sie tauchen auch später immer wieder im Mathe-Unterricht auf. Selbst beim Beweis des Satzes von Pythagoras können die Formeln hilfreich sein.
Und wofür braucht man die binomischen Formeln im wirklichen Leben?
Wenn man nicht gerade Mathe Lehrer ist, der seine Schüler mit entsprechenden Beweisen beglücken darf, dann wird es eng mit den praxisnahen Anwendungen für binomische Formeln. Vielleicht benötigt sie ein Naturwissenschaftler beim Umstellen von Formeln, doch gefühlt haben 99% aller Berufe nichts mehr damit zu tun. Persönlich nutze ich die Formeln höchstens noch zum Kopfrechnen. Und als Thema für mein Blog 😉
Bildquelle der Binomischen Formeln: geralt (Photoopia)