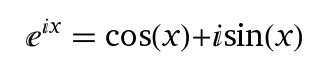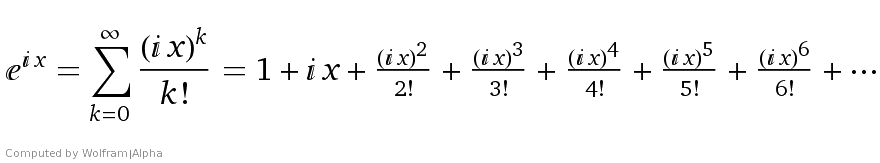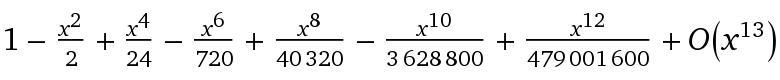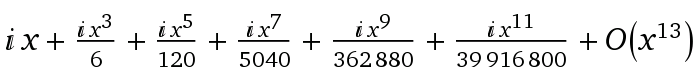Euler-Formel / Eulersche Identität

Im Jahre 1748 bewies Leonhard Euler im Rahmen seines Werkes Introductio in analysin infinitorum die sogenannte Eulersche Identität. Für reelle Zahlen x gilt folgende Gleichung:

Eulers Formel verbindet im Komplexen Zahlenraum die natürliche Exponentialfunktion e^x mit den trigonometrischen Funktionen sin(x) und cos(x). Das ist erst einmal ziemlich verblüffend und alles andere als trivial. Erkennbar wird der Zusammenhang aber ganz gut mit Hilfe der Taylorreihen-Entwicklung der jeweiligen Funktionen.

Die Potenzreihen von Cosinus(i*x) und Sinus(i*x) ähneln stark der von e^{i x}.

Wer genau hinsieht und i² = -1 berücksichtigt, der wird erkennen, dass sich die Komponenten der Sinus und Cosinus Reihe genau zu den Komponenten der E-Funktionsreihe aufaddieren lassen. Die Herleitung über die Potenzreihen bildet auch die Grundlage für den Beweis der Euler Formel.

Ein Spezialfall der Eulerschen Formel bzw. Identität ist der Fall x=π. Wenn wir die Kreiszahl pi in die Eulersche Gleichung einsetzen so erhalten wir

e^i*π = -1

Wenn das nicht mal wirklich verblüffend ist …

Ist das nicht schön? Noch schöner wird es nach einer leichten Umformung: e^πi + 1 = 0. Diese Anwendung der Euler-Formel vereint fünf der wichtigsten Zahlen der Mathematik in einer Formel. Oftmals wird auch bei dieser besonderen Gleichung von der Eulerschen Identität gesprochen.